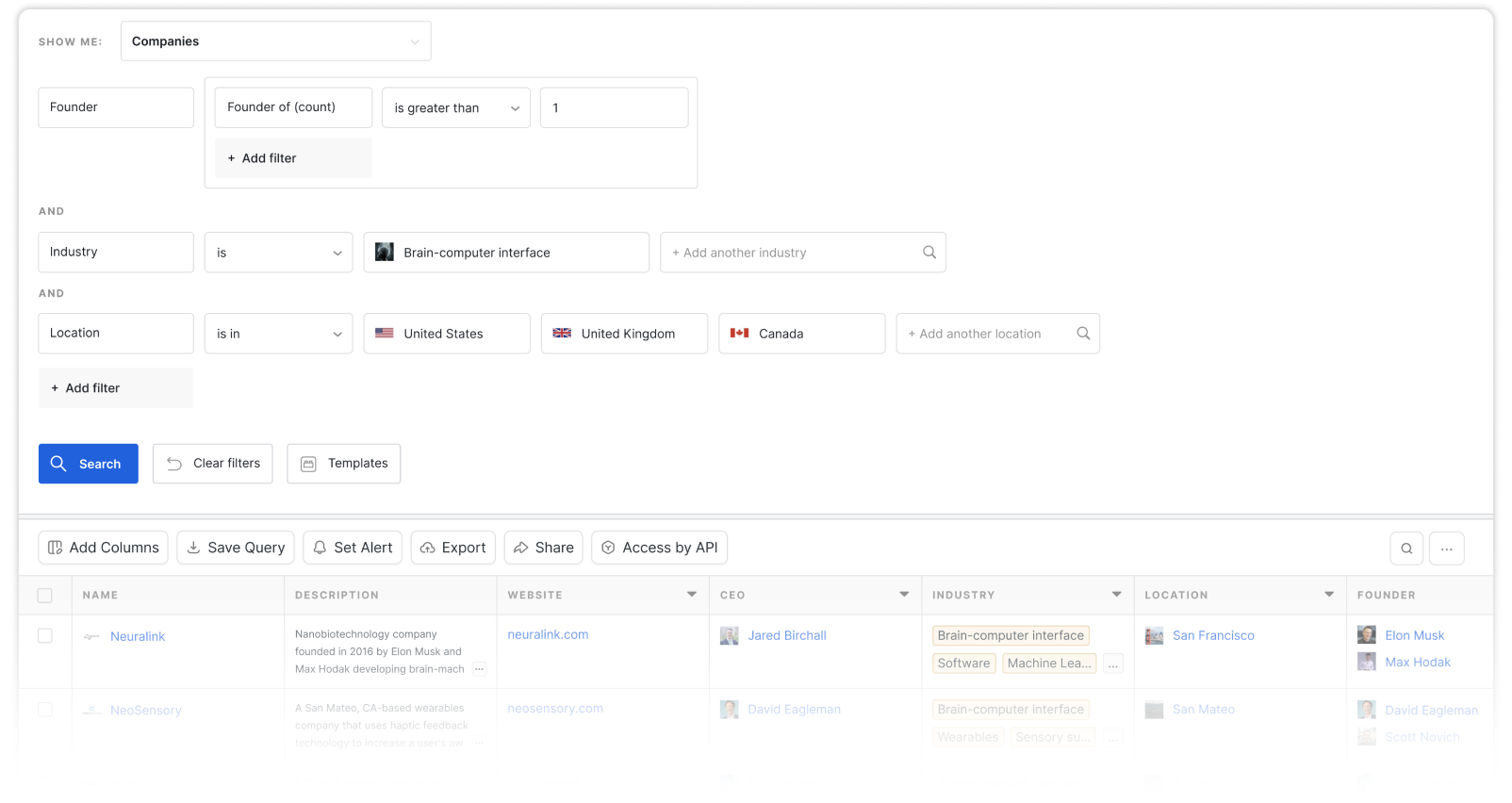
Other attributes
Spectral clustering is a simple implementation of clustering that can be solved efficiently by standard linear algebra software, and it has been shown to outperform other clustering algorithms such as k-means in some circumstances.
Spectral clustering algorithms typically follow 3 main steps:
- Pre-processing: Compute a similarity graph and represent it with an adjacency matrix which has a similarity between each vertex and its elements.
- Data decomposition: Compute the eigenvalues and eigenvectors of the matrix using a Graph Laplacian. Then, map the data points into lower-dimensional space based on one or more of the eigenvectors.
- Grouping: Use k-means to cluster these data points into k clusters.
Spectral clustering is easy to implement, reasonably fast for sparse data sets having several thousand elements, and it provides good clustering results. Unlike, k-means and other common clustering techniques, spectral clustering doesn't make strong assumptions on the statistics of the clusters, which can help create more accurate clusters when those strong assumptions aren't relevant.
For larger data sets, however, spectral clustering is computationally expensive and can be more complex to implement.